Flandre Scarlet's Blog

自古T3出神题！自古3面出神曲！

我觉得这次T3的题很符合我的胃口←_←

题意：给定一个图，求两点间所有路径上最小边权的最大值。

初中写只会二分答案+判断连通性（能再蠢些么= =）

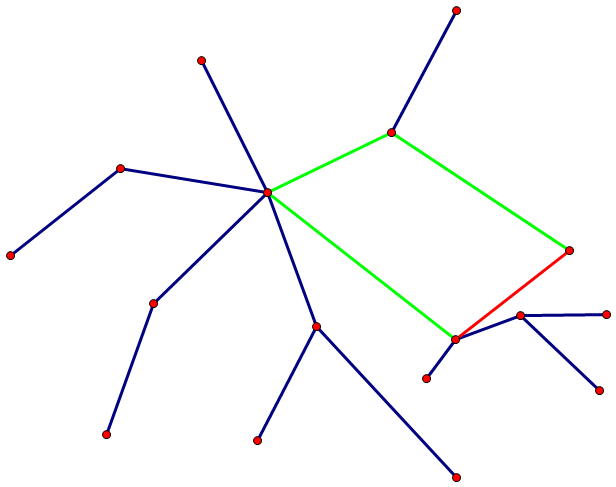
看了题解：该边一定出现在最大生成树上！（如下图，蓝、绿色表示最大生成树。若所求边边（红色）不在最大生成树上，则绿边上必有所有边权必大于红边（想想Kruskal），则路径可以优化）只需求树上路径的最小边权。

于是学了欢乐的树上倍增算法（基于LCA）。

先说LCA（最近公共祖先）：即找树上两点公共祖先中最近的一个。

姿势：预处理出树上第i点往上寻2^j的节点编号（dfs+伪分治），存入p[i][j]。

若询问两点a、b高度相同，则从较大的j往下枚举至0，一旦p[a][j]！=p[b][j]则两点都往上跳2^j层（即a=p[a][j],b=p[b][j]），那么最后p[a][0]即所求答案。……①

若询问两点a、b高度不同，则让较深的一点按照上述姿势往上调至相同高度。……②

辣么问题来了，求路径最小边权怎么搞。

是时候表演真正的技术了：预处理出树上第i点往上寻2^j个节点路径上的最小值，在①②往上跳的过程中同步维护整个路径最小边权，KO（BTW：树上路径长度也是这么做的）

CODE（我写得奇丑无比）：

#include<cstdio>
#include<cstring>
#include<algorithm>
#define maxm 50010
#define maxn 10010
#define INF 2000000000
using namespace std;

struct Edge
{
	int u,v,w;
};
Edge edges[maxm];
int r[maxm],n,m,f[maxn];
int GF(int x)
{
	return f[x]==x?x:f[x]=GF(f[x]);
}
int cmp(int a,int b)
{
	return edges[a].w>edges[b].w;
}
Edge Gra[maxn*2];int Size=0;
int next[maxm],first[maxn];
void AddEdge(int u,int v,int w)
{
	int m=++Size;
	Gra[m]=(Edge){u,v,w};
	next[m]=first[u];
	first[u]=m;
}
int p[maxn][15];//以i跳2^j格的点（交的时候用14也让我水过了，看来没用链卡我）
int w[maxn][15];//跳的范围内最小边权
int h[maxn];//每点深度= =
int dfs(int u)
{
	for (int i=first[u];i!=-1;i=next[i])
		if (!h[Gra[i].v])
		{
			Edge e=Gra[i];
			h[e.v]=h[u]+1;
			p[e.v][0]=u;
			w[e.v][0]=e.w;
			dfs(e.v);
		}
}
void init()
{
	for (int j=1;(1<<j)<=n;j++)
		for (int i=1;i<=n;i++)
			if (p[i][j-1]!=-1)
			{
				p[i][j]=p[p[i][j-1]][j-1];
				w[i][j]=min(w[i][j-1],w[p[i][j-1]][j-1]);
			}
}
int LCA(int a,int b)
{
	int i,ans=INF;
	if (GF(a)!=GF(b)) return -1;
	if (h[a]<h[b]) swap(a,b);
	for (i=0;(1<<i)<=h[a];i++);
	i--;
	for (int j=i;j>=0;j--)
		if (h[a]-(1<<j)>=h[b])
		{
			ans=min(ans,w[a][j]);
			a=p[a][j];

		}
	if (a==b) return ans;
	for (int j=i;j>=0;j--)
	{
		if (p[a][j]!=-1&&p[a][j]!=p[b][j])
		{
			ans=min(ans,w[a][j]);
			a=p[a][j];
			ans=min(ans,w[b][j]);
			b=p[b][j];
		}
	}
	ans=min(ans,w[a][0]);
	return min(ans,w[b][0]);
}
int main()
{
	scanf("%d%d",&n,&m);
	for (int i=1;i<=n;i++)f[i]=i;
	for (int i=1;i<=m;i++)r[i]=i;
	for (int i=1;i<=m;i++)
	{
		int u,v,w;scanf("%d%d%d",&u,&v,&w);
		edges[i]=(Edge){u,v,w};
	}
	sort(r+1,r+1+m,cmp);
	for (int i=1;i<=n;i++)
		first[i]=-1;
	for (int i=1;i<=m;i++)
	{
		Edge e=edges[r[i]];
		int x=GF(e.u),y=GF(e.v);
		if (x!=y)
		{
			f[x]=y;
			AddEdge(e.u,e.v,e.w);
			AddEdge(e.v,e.u,e.w);
		}
	}
	h[1]=1;
	dfs(1);
	init();
	int q;
	scanf("%d",&q);
	for (int i=1;i<=n;i++)
		if (!h[i]) h[i]=INF;
	for (int i=1;i<=q;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		printf("%d\n",LCA(u,v));
	}
	return 0;
}